An example of a system of two linear equations is shown below We use a brace to show the two equations are grouped together to form a system of equations {2x y = 7 x − 2y = 6 A linear equation in two variables, such as 2x y = 7, has an infinite number of solutions Its graph is Find the number of students in each class QUse the method of substitution to solve each other of the pair of simultaneous equation 1} x4y=4 and 3y5x=1 QUse the method of substitution to solve each other of the pair of simultaneous equation 1} 2x9y=9 and 5x2t=27 Please solve 2x3y=12, 2x3y=6 13d16g=6 & 32d25g=30solveSolve by Addition/Elimination x2y=3 2x3y=9 x − 2y = 3 x 2 y = 3 2x − 3y = 9 2 x 3 y = 9 Multiply each equation by the value that makes the coefficients of x x opposite (−2)⋅ (x−2y) = (−2)(3) ( 2) ⋅ ( x 2 y) = ( 2) ( 3) 2x−3y = 9 2 x 3 y = 9 Simplify Tap for more steps Simplify ( − 2) ⋅ ( x − 2 y

3 X 1 Y 9 0 2 X 3 Y 5 Mathematics Topperlearning Com G53lykpp
3/x-1/y 9=0 2/x 3/y=5 by elimination method
3/x-1/y 9=0 2/x 3/y=5 by elimination method-Algebra Systems of Equations and Inequalities Linear Systems with Multiplication 1 Answer maganbhai P #x=1 and y=2# Which method do you use to solve #x=3y# and #x2y=3#?You can't solve this system You have two equations and three variables X and x are NOT the same thing
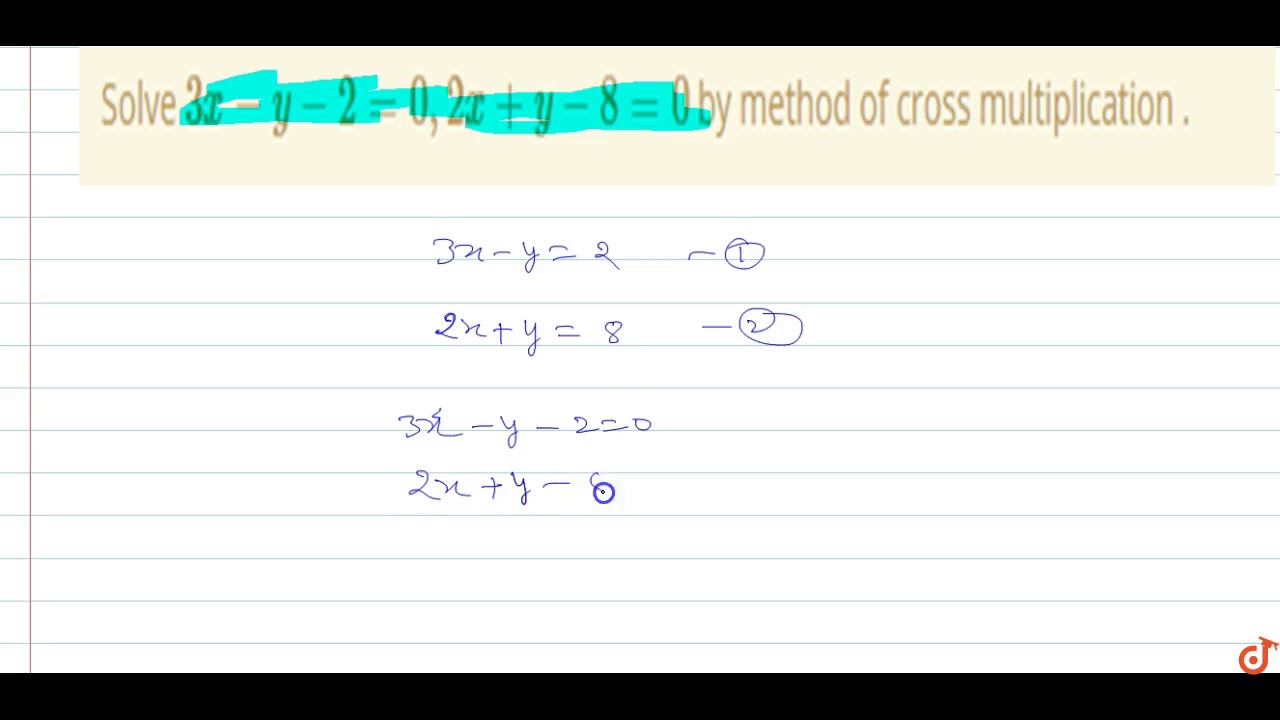



Solve 3x Y 2 0 2x Y 8 0 By Method Of Cross Multiplication Youtube
I have five similar math questions that I need help on if possible &n bsp; Solve the following system of equations graphically 2x 3y 6 = 0 2x 3y 18 = 0 Also, find the area of the region boundedWrite down the steps involved in the elimination method Step 1 At first, we select a variable which we want to eliminate from the equations Step 2 Take suitable constants and multiply them with the given equations so as to make the coefficients of the
9x – 2 (9) = 108 x = 14 Answer x = 14 and y = 9 Please log in or register to add a commentLet 1/√x=a Let 1/√y=b then, 2a3b=2 eqn 1 4a–3b=1 eqn2 Adding eqn 1 and eqn 2 2a4a3b3b=1 6a=1 a=1/6 1/√x=1/6 √x=6 x=36 Substituting a=1/6 in eqn1 2(1/6)3b=2 3b=2(1/3) b=5/9 1/√y=5/9 y=81/253x/ 25y/3=7/3 say eqn2 To eliminate x by multiplying 3 in eqn1 and multiplying by 1 in eqn2 3x/2–3y/2=0 →say eqn1 3x/ 25y/3=7/3→say eqn2 Then, subtract eqn2 from eqn1,we get value of y –3y/2 (5y/3) = 0 –7/3 –3y/2 5y/3 = 7/3 y/6 = 7/3 y = 14,
9x 3y = 9 asked in Linear Equations by Anika01 ( 571k points) linear equations in y = 2 x = 1 We can solve this one of two ways;The elimination method for solving systems of linear equations uses the addition property of equality You can add the same value to each side of an equation So if you have a system x – 6 = −6 and x y = 8, you can add x y to the left side of the first equation and add 8 to the right side of the equation And since x y = 8, you are adding the same value to each side of the first




5 X 3 Y 1 3 2x 2 3y 5 Brainly In




Question 2 Solve The Following System Of Linear Chegg Com
Extract the matrix elements x and y 3x2y=5,5x3y=2 In order to solve by elimination, coefficients of one of the variables must be the same in both equations so that the variable will cancel out when one equation is subtracted from the other 5\times 3x5\left (2\right)y=5\times 5,3\times 5x3\times 3y=3\times 2Solve by Addition/Elimination xy=3 , xy=7 x y = 3 x y = 3 , x y = 7 x − y = 7 Multiply each equation by the value that makes the coefficients of x x opposite x y = 3 Transcript Ex 33, 1 Solve the following pair of linear equations by the substitution method (i) x y = 14 x – y = 4 x y = 14 x – y = 4 From equation (1) x y = 14 x = 14 – y Substituting value of x in equation (2) x – y = 4 (14 – y) – y = 4 14 – y – y = 4 14 – 2y = 4 –2y = 4 – 14 –2y = –10 y = (−10)/(−2) y = 5 Putting y = 5 in (2) x – y = 4 x = y 4 x




Ncert Solutions Class 10 Maths Ch 3 Pair Of Linear Equations In Two Variables Edu Spot




What Is The Solution For An Equation Of A Line Passing Through The Point Of Intersection Of 2x 3y 5 0 And 7x 5y 2 0 And Parallel To The Lines 2x 3y 14 0 Quora
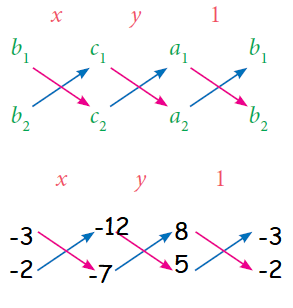
Elimination method First multiply one or both the equations by some suitable nonzero constants to make the coefficients of one variable numerically equal then add or subtract one equation from the other so that one variable gets eliminated (i) What is the Known? q solve x y 3 and 2x 5y 10 using elimination method Mathematics TopperLearningcom 0yujch00\(x y = 5 \\2x 3 y= 4 \) Steps Elimination method




3 2 Solving By Substitution Or Elimination N



1
Let us use elimination method to solve the given system of equations Multiply (2) by 3 And subtract both the equations From (1);For solving pair of equation, in this exercise use the method of elimination by equating coefficients 3 (x 5) = y 2 2 (x y) = 4 3y Ex 34, 1 (Elimination) Solve the following pair of linear equations by the elimination method and the substitution method (i) x y = 5 and 2x – 3y = 4 x y = 5 2x – 3y = 4 Multiplying equation (1) by 2 2(x y) = 2 × 5 2x 2y = 10 Solving




3 X 1 Y 9 0 2 X 3 Y 5 Mathematics Topperlearning Com G53lykpp
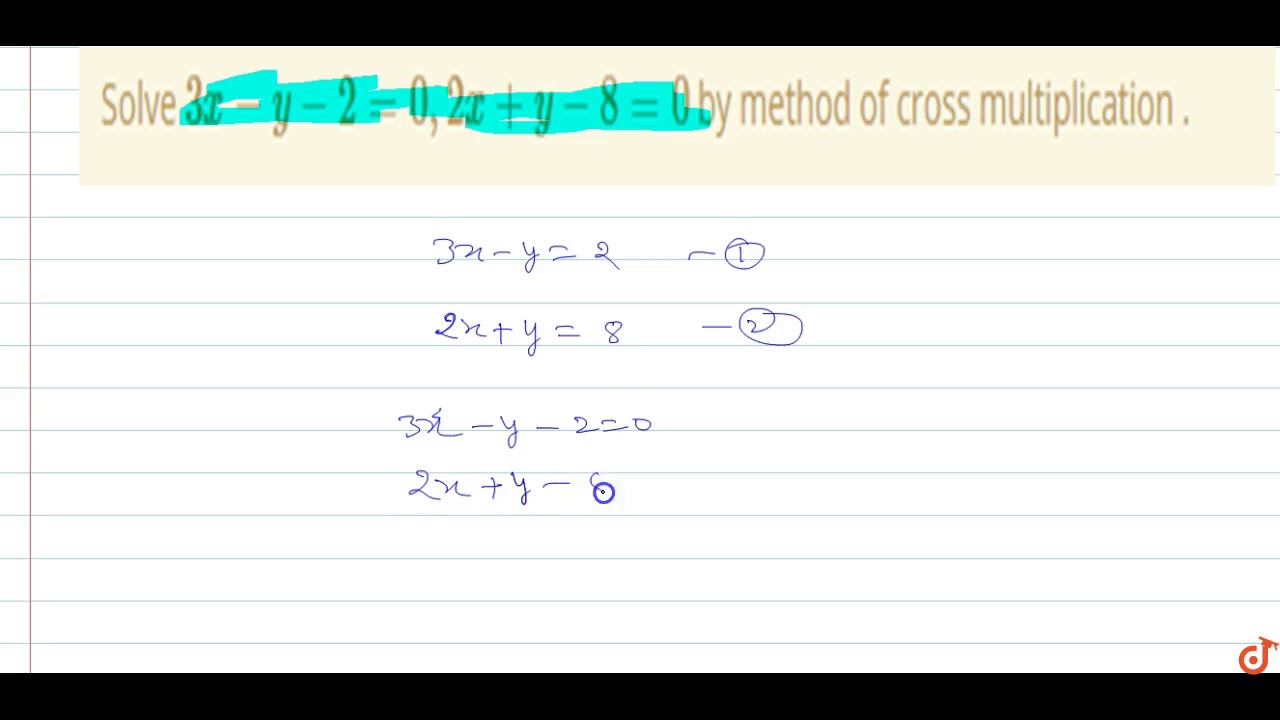



Solve 3x Y 2 0 2x Y 8 0 By Method Of Cross Multiplication Youtube
Let xy=7 be (1) and 2x6y=10 be (2) Multiply (1) by 6 to get 6x6y = 42 (3) Add (2) and (3) 8x = 32, or x = 4 From (1) y = 7x = 7–4 = 3 Hence, x = 4 and y = 3 Use the elimination method 1) 3xy=1 5xy=9 2) 4x6y=24 4xy=10 3)2xy=3 x3y=16 4) 2x3y=7 3x4y=10 1 See answer mandaa97 is waiting for your help Add your answer and earn points Substitution method 1) The system of equations are y = 5y 1 and 2y 10 = 3 The above system of equations have only one variable that is y, so system of equations has no solution Solve the each equation separately for y Solve the equation 1 y = 5y 1 y 5y = 1 4y = 1 y = 1/4 Solve the equation 2 2y 10 = 3 2y = 3 10



1



Step By Step Math Wolfram Alpha Blog
Free system of equations elimination calculator solve system of equations unsing elimination method stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie PolicyBy elimination or by substitution I don't know which one is your preferred method so I will do both Both methods will yield the same answer Method 1 Elimination 2xy =0 x 2y = 5 Let us use x as the variable we want to work out; cocept of elimation method The sum of the digits of a two digit number is 12 The number obtained by interchanging Its digits exceed the given number by 18 find the number pxqy=pq qxpy=pq x2y=5 3x/23y=10 solve by elimination method
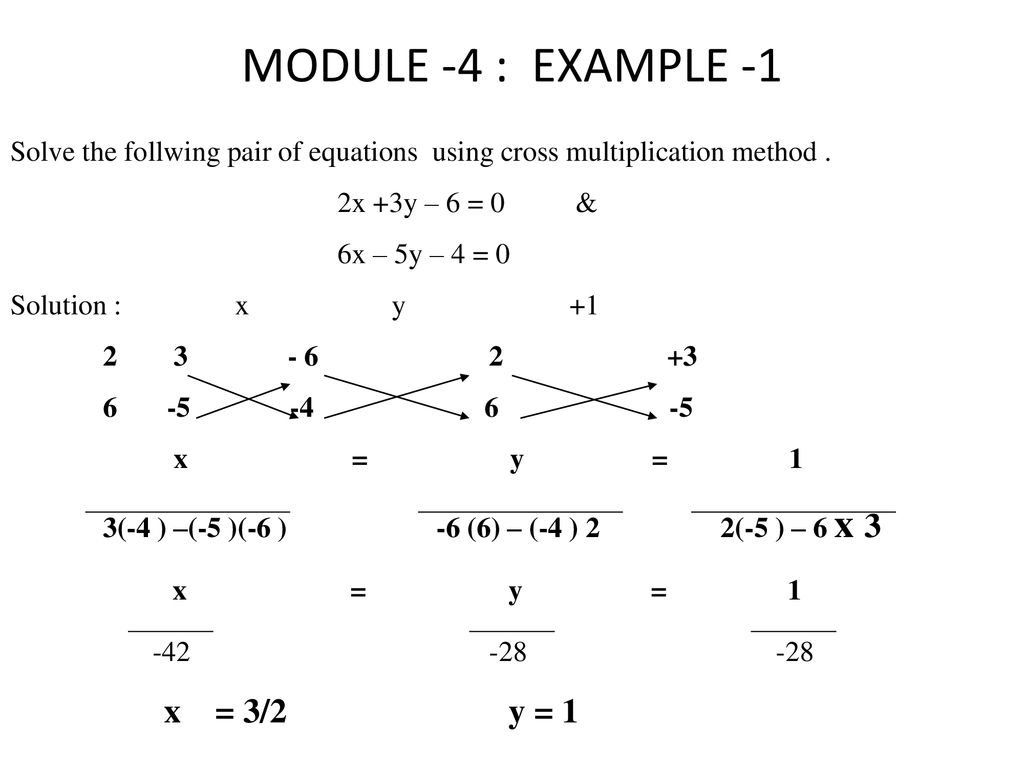



Topic Pair Of Linear Equtions In Two Variables Ppt Download




Pair Of Linear Equations In Two Variables Equations Cbse Class 10 Ekshiksha
Click here👆to get an answer to your question ️ Solve the equation by substitution method 2x 3y = 9 , 3x 4y = 5 using Gaussian or GaussJordan Elimination x y z = 5 2x – 3y 6z = 32 4x 5y 10z = 8 asked in ALGEBRA 2 by anonymous gaussjordanmethod2 x 3 2 y = − 1 and x and hence find out 2 a b EASY View Answer Solve the following pairs pf linear (simultaneous) equations using method of elimination by substitution 2 (x




3 2 Solving By Substitution Or Elimination N



Solve For X And Y X 1 2 Y 1 3 9 X 1 3 Y 1 2 8 Sarthaks Econnect Largest Online Education Community
Share It On Facebook Twitter Email 1 Answer 0 votes answered by AmirMustafa (600k points) selected by Vikash Kumar Best answer The given equations are Example 18 Solve the following pair of equations by reducing them to a pair of linear equations 5/(𝑥 −1) 1/(𝑦 −2) = 2 6/(𝑥 −1) – 3/(𝑦 −2) = 1 5/(𝑥 − 1) 1/(𝑦 − 2) = 2 6/(𝑥 − 1) – 3/(𝑦 − 2) = 1 So, our equations become 5u v = 2 6u – 3v = 1 Thus, our Transcript Example 7 Solve the following pair of equations by substitution method 7x – 15y = 2 x 2y = 3 7x – 15y = 2 x 2y = 3 From (1) 7x – 15y = 2 7x = 2 15y x = (𝟐 𝟏𝟓𝒚)/𝟕 Substituting the value of x in (2) x 2y = 3 (2 15𝑦)/7 2𝑦=3 Multiplying both sides by 7 7 × ((2 15𝑦)/7) 7×2𝑦=7×3 (2 15y) 14y = 21 15y 14y = 21 – 2 29y = 21 – 2



Systems Of Linear Equations




If 3x 5y 9 And 5x 3y 7 Then Find The Value Of X Y Youtube
Solving linear equations using elimination method Solving linear equations using substitution method Solving linear equations using cross multiplication method Solving one step equations Solving quadratic equations by factoring Solving quadratic equations by quadratic formula Solving quadratic equations by completing square Solve the following pair of linear equations by substitution method 3x – y = 3;Solve by elimination method 6x9y=195 and 7y2y=85/ The second problem Solve by elimination method 03x02y=4 and 04x read more



Simultaneous Equations Gmat Math Study Guide




Ex 3 4 1 Solve By Elimination And Substitution I X Y 5 2x 3y
4x −5y = − 1 (lets call it "1") and 2x y = 5 then 4x 2y = 10 (lets call it "2") (Subtract 2 from 1) −7y = − 11 y = 11 7 Hence Solve the following systems of equations 2/x 3/y = 9/xy 4/x 9/y = 21/xy, where, x ≠ 0, y ≠ 0 asked Apr 26 in Statistics by Haifa ( k points) pair of linear equations in two variablesGet an answer for 'If 2x3y= 5 and x3y= 4 find the values of x and y' and find homework help for other Math questions at eNotes




Maths Class 10 Pages 51 100 Flip Pdf Download Fliphtml5



Cbse 10 Math Cbse Linear Equations In Two Variables Ncert Solutions
About Elimination Use elimination when you are solving a system of equations and you can quickly eliminate one variable by adding or subtracting your equations together You can use this Elimination Calculator to practice solving systemsFirst, you have to equate the coefficients of the y so equation 1 will be doubled 4x 2y = 0 x 2yLearn how to solve differential equations problems step by step online Solve the differential equation dy/dx= ( (y1) (x2)* (y3))/ ( (x1) (y2)* (x3)) Group the terms of the differential equation Move the terms of the y variable to the left side, and the terms of the x variable to the right side Simplify the expression \frac {y2} {y1




Selina Chapter 6 Linear Equations Including Problems Icse Solutions Class 9 Maths




Linear Equations Assignment 10 System Of Linear Equations Equations
Find an answer to your question 3/x 1/y= 9 and 2/x 3/y = 5 the simple interest on a certain sum of money for 5 years is 4500 what is the simple interest on the same sum of money for 3 years at the same rate of2 x − 9 y = 6, 7 x 3 y = 5 MEDIUM View Answer Solve the equation using elimination method Solve the following system of equations using elimination method2 algebraic methods (elimination and substitution) and graphical method Elimination 2x 3y = 5 So 6x 9y = 15 (equation 1) 3x y = 4 6x 2y = 8 (equation 2) (6x 9y) (6x 2y) = 15 8 7y = 7 y = 1 (equation 3) Substitute y = 1 into equation 2, 3x (1) = 4 x = 1 (x, y) = (1, 1) Substitution 2x 3y = 5 (equation 1) 3x y = 4, so y = 4 3x (equation 2)




Numerical Computing Question Bank Unit I Q 1 Solve By Raisoni




Topic Pair Of Linear Equtions In Two Variables Ppt Download
Steps for Solving Linear Equation 2x3y = 5 2 x 3 y = 5 Subtract 2x from both sides Subtract 2 x from both sides 3y=52x 3 y = 5 − 2 x Divide both sides by 3 Divide both sides by 3 3/x 1/y 9 = 0, 2/x 3/y = 5 linear equations in two variables;Click here to see ALL problems on Linearsystems Question solve the linear system using elimination xy=5 Xy=3 Answer by solver () ( Show Source ) You can put this solution on YOUR website!
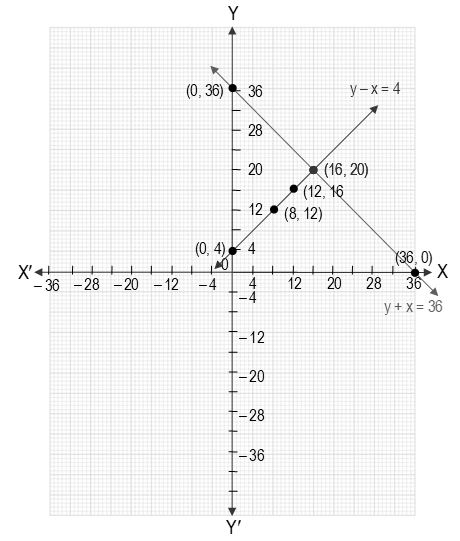



Pair Of Linear Equations In Two Variables




Ppt Simultaneous Equations Powerpoint Presentation Free Download Id
Question hi, can you please help me solve this problem using the elimination method 1 3x2y=5 2x3y=12 2 4x3y3=0 8x=9y1 this ones either substitution, elimination or comparison methodsXy=5(1) 2xy=9(2) Take eq(1) y=5x(3) Put value of y in eq(2) 2x(5x)=9 2x5x=9 x5=9 x=9–5 x=4 Put value of x in eq(3) y=5–x y=5–4 y=1 (x=4, y=1)The Elimination Method Another way to algebraically solve a system of equations is by eliminating a variable This process involves adding or subtracting the equations, depending on whether the terms are opposites (then add) or the same (then subtract) First put both equations into standard form (Ax By = C) Elimination Using Addition




Solve The Following System Of Equation 2x 3y 8 0 4x 5y 14 0




Solving Simultaneous Equations Equations And Inequalities Siyavula
How do you solve the system using the elimination method for 3x – 2y – 7 = 0 and 5x y 3 = 0? Solve the following pair of linear (Simultaneous ) equation using method of elimination by substitution 2( x – 3 ) 3( y – 5 ) = 0 5( x – 1 ) 4( y – 4 ) = 0 Answer Given equations are 2( x – 3 ) 3( y – 5 ) = 0 (1) 5( x – 1 ) 4( y – 4 ) = 0 (2) From (1), we getPair of Linear Equations in Two Variables Reducing a Pair of Equations to Linear Form If 3/x 2/y = 5 and 4/x
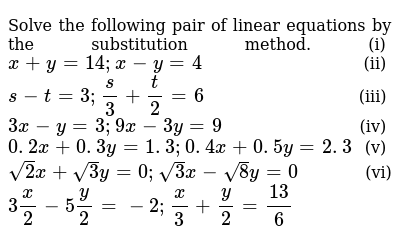



Solve The Following Pair Of Linear Equations By The Substitut



Q Tbn And9gct3yn1gvmbccfl57svv3if3x1gxfchbodcvpyuv6enbs7fkzqum Usqp Cau
To solve it by elimination method, let us multiply second equation by 3 3x — 3y = 3 equation 3 Now add first and third equation 5x = 15 x = 3 From equation 2, y = x1 y = 2 Hence x = 3, y = 2 (b) 3x y = 10 Since we have one equation and 2 variables, it cannot be solved by elimination method To solve this, we can go for trial and error5x2y=3,x5y=4 To solve a pair of equations using substitution, first solve one of the equations for one of the variables Then substitute the result for that variable in the other equation 5x2y=3 Choose one of the equations and solve it for x by isolating x




Solve The Equation By Elimination Method 0 08x 0 09y 186 Scholr




Graphically The Pair Of Equations 6x 3y 10 0 2x
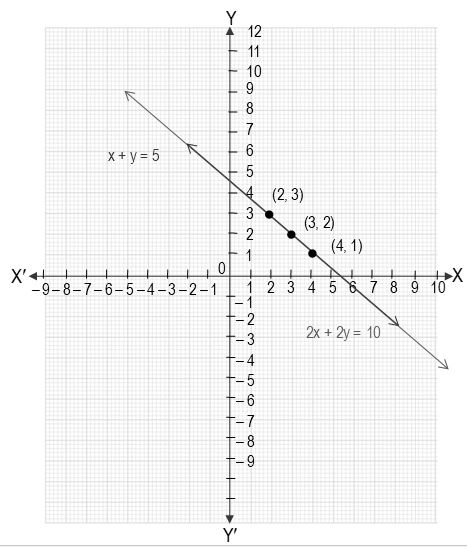



Pair Of Linear Equations In Two Variables



Solving Equations Algebraically



Http Maths Dur Ac Uk Users Daniel Evans Mes Messolutionsupdated Pdf




Gauss Jordan Elimination Reduces To Row Echelon Form Always Mathematics Stack Exchange




Pair Of Linear Equations In Two Variables Class 10 Extra Questions Maths Chapter 3 With Solutions Answers




Ssc Mathematics Chapter 4 Pair Of Linear Equations In Two Variables




Gseb Solutions For Class 10 Mathematics Pairs Of Linear Equations In Two Variables Cbse Tuts




Mathematics For The Ib Diploma Analysis And Approaches Sl Draft Copy By Hodder Education Issuu




Solve By Cross Multiplication X 2y 1 0 2x 3y 12 0 Youtube




Solve The Pair Of Linear Equations 3x 2y 11 0 2x 3y 10 0 By Substitution Method Brainly In



Systems Of Linear Equations




Pair Of Linear Equations In Two Variables Equations Cbse Class 10 Ekshiksha




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 5




Solving A System Of Equations Using A Matrix Precalculus Socratic




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 4




5 X 1 1 Y 2 2 6 X 1 3 Y 2 1 By Elimination Method Brainly In




2 Use Cramer S Rule To Solve The Following Set Of Chegg Com
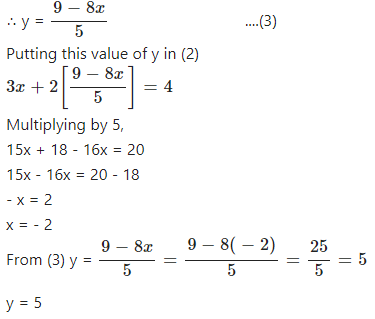



Simultaneous Linear Equations Class 9th Concise Selina Icse Maths Icsehelp




Maths Class 10 Pages 51 100 Flip Pdf Download Fliphtml5




Solve Solve Linear And Quadratic Equations With Step By Step Math Problem Solver



Canvas Bham Ac Uk Courses Files Download Verifier Olsyulszmw31bkuumjmm1h3moiw4myavdszsni9s Wrap 1



Solving Equations Using Cross Multiplication Method




7x 3y 1 0




Solving Linear Systems By Elimination




Ex 3 4 1 Solve By Elimination And Substitution I X Y 5 2x 3y



If 2x 3y 17 And 3x 5y 27 What Are X And Y Quora
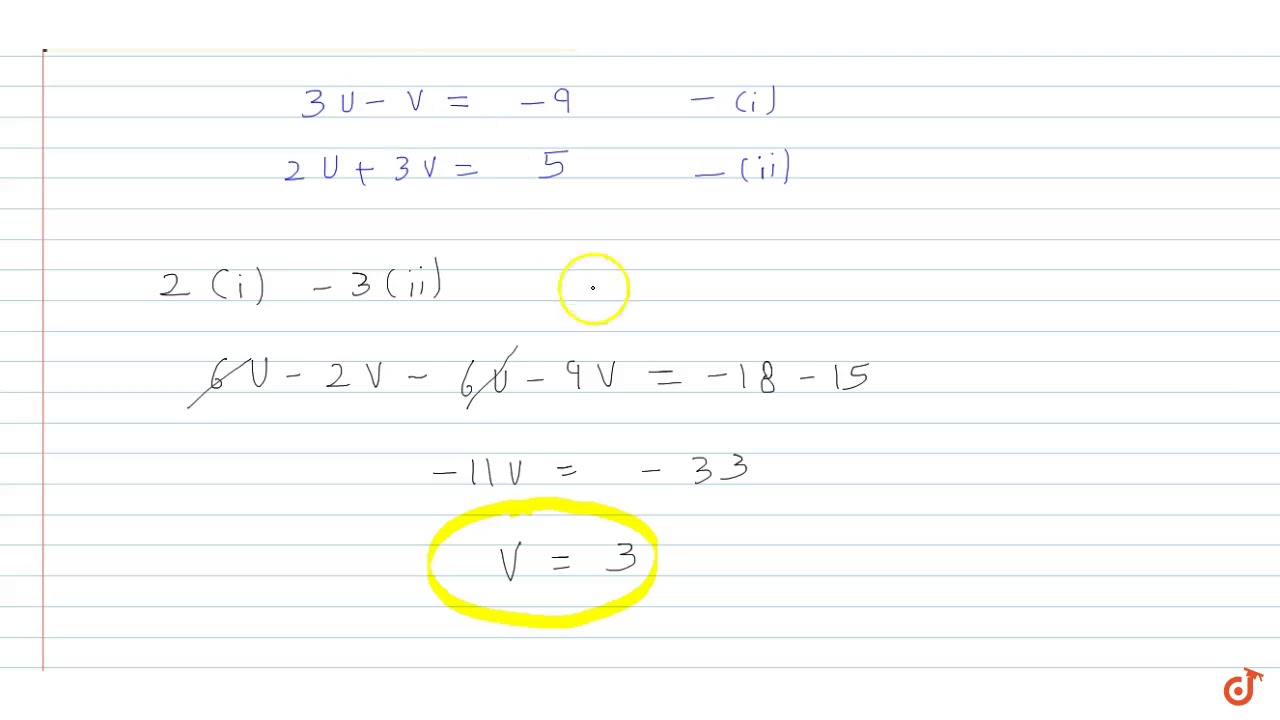



3 X 1 Y 9 0 2 X 3 Y 5 0 Y 0 Youtube




Module 1 Plane Coordinate Geometry



Solve For X And Y 3 X 1 Y 9 0 2 X 3 Y 5 Sarthaks Econnect Largest Online Education Community



Www Oup Com Au Data Assets Pdf File 0023 571 Im10 51 52 Ch6 Simultaneous Equations Pdf



Www Waynesville K12 Mo Us Cms Lib07 Mo Centricity Domain 603 A1 c6 l2 solution key worked out Pdf



Cbse 10 Math Ncert Solutions




Solve By Elimination Method 1 5 X 2 1 4 1 Y 4 X 2 5 1 Y Maths Linear Inequations Meritnation Com



Www Oup Com Au Data Assets Pdf File 0023 571 Im10 51 52 Ch6 Simultaneous Equations Pdf




Solving Linear Systems



Q Tbn And9gcrygwftvdewimeeqi 3oi1ubfj2imi1hvdrfvy3mevtavogo7cv Usqp Cau




2x 3y 9 3x 4y 5 Solve By Elimination Method Brainly In
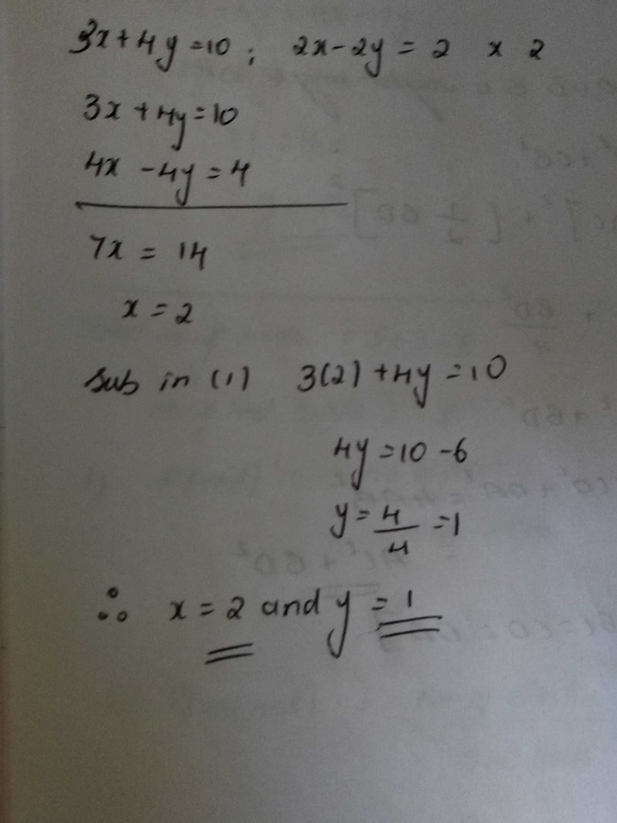



Solve Elimination Method 3x 4y 10 And 2x 2y 2 Scholr



The Substitution Method




1 Topic The Substitution Method 2 Topic The Substitution Method California Standard 9 0 Students Solve A System Of Two Linear Equations Ppt Download




無料ダウンロード 3x 2y5 X5 Y



Www Cimt Org Uk Projects Mepres Step Up Mepanswers Pdf




Step By Step Math Wolfram Alpha Blog




Solving Simultaneous Equations Equations And Inequalities Siyavula
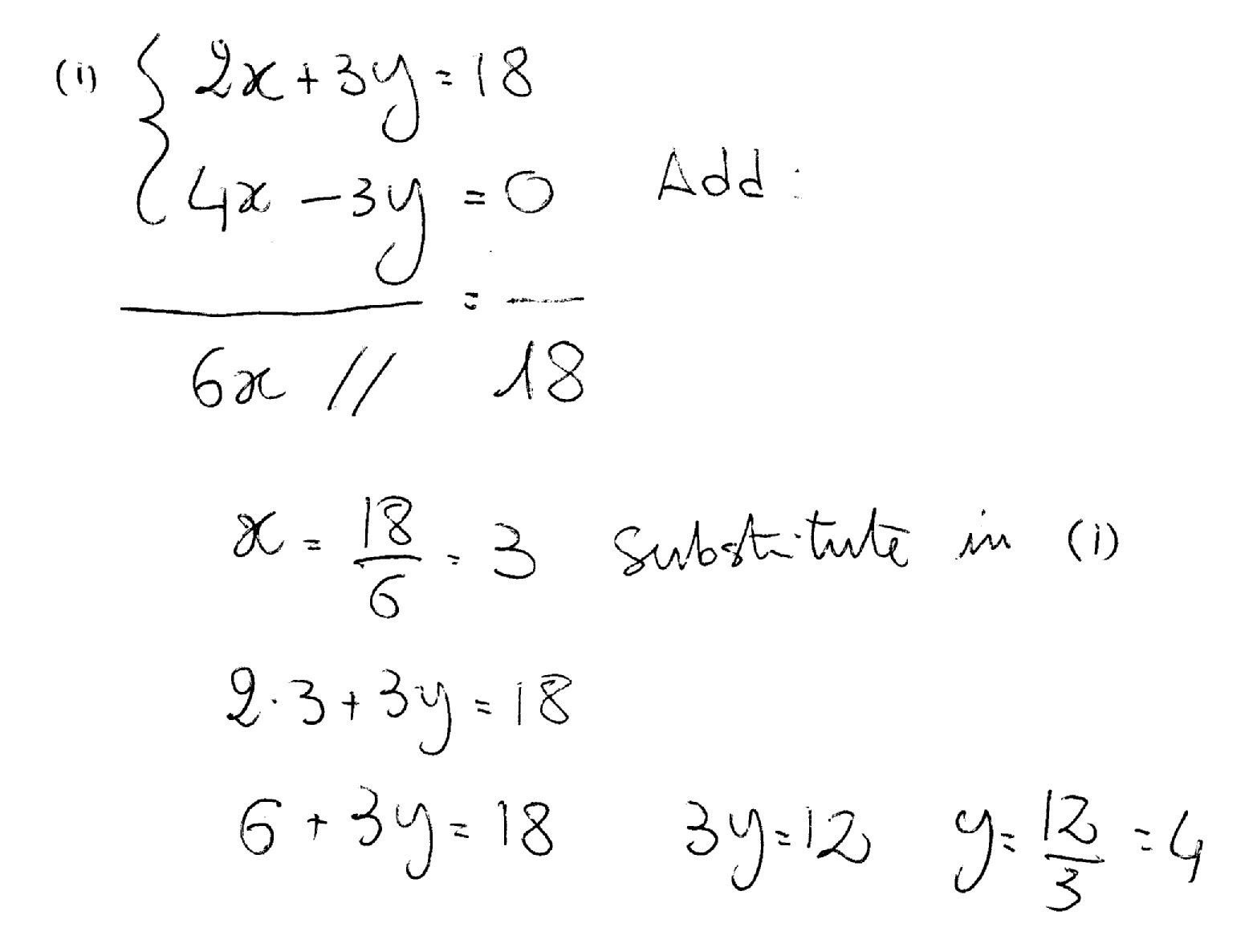



How Do You Solve The System 2x 3y 18 And 4x 3y 0 Socratic
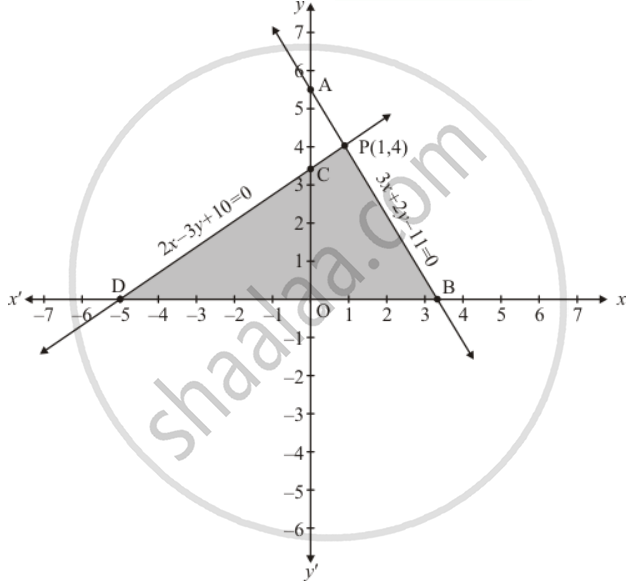



Solve The Following System Of Linear Equations Graphically And Shade The Region Between The Two Lines And X Axis 3x 2y 11 0 2x 3y 10 0 Mathematics Shaalaa Com




Ssc Mathematics Chapter 4 Pair Of Linear Equations In Two Variables
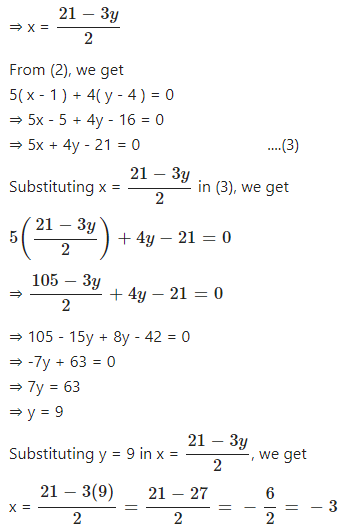



Simultaneous Linear Equations Class 9th Concise Selina Icse Maths Icsehelp




Answers



Solving Systems Of Equations



Www Keble Ox Ac Uk Wp Content Uploads Ch 1 Algebra Pdf




Pycse Python3 Computations In Science And Engineering




Cbse Ncert Solution For Class 10 Maths Linear Equations In 2 Variables



The Substitution Method




Ex 3 3 1 Solve By Substitution Method I X Y 14 Ex 3 3




3 X 1 Y 9 And 2 X 3 Y 5 By Elimination Method Brainly In




Solving A System Of Equations Using A Matrix Precalculus Socratic




X 2y 3 2 2x Y 3 2 By Substitution Method Novocom Top



Chapter 9 Systems Of Equations And Matrices Manualzz




Algebraic Elimination Method Class 10 Ncert Solutions Suresolv



Rd Sharma Solutions For Class 10 Chapter 3 Pair Of Linear Equations In Two Variables



R D Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 2




3 X 1 Y 9 2 X 3 Y 5 Solve Using Elimination Method Mathematics Topperlearning Com T5ibnqll




Math 163 Online Problems Supplemental Lessons On Gaussian




Solve Equations Using Substitution Method 2x Y 3 And 4x Y 3




Graphically The Pair Of Equations 6x 3y 10 0 2x




Systems Of Equations With Elimination 3y 4x 11 Y 2x 13 Video Khan Academy



Www Sfdr Cisd Org Media 7739 Drfs Algebra 1 Pdf



Solve The Following Systems Of Equations 2 X 3 Y 9 Xy 4 X 9 Y 21 Xy Where X 0 Y 0 Sarthaks Econnect Largest Online Education Community



What Is The Answer To Find The Equation Of A Straight Line Through The Point Of Intersection Of Lines 2x 3y 5 0 And 3x 4y 7 0 Which Is Parallel To The Line 2x Y 2 0 Quora




Ex 3 4 1 Solve By Elimination And Substitution I X Y 5 2x 3y




Solutions To Problems In Chapter One Mathematics



0 件のコメント:
コメントを投稿